What’s an eigenvector and eigenvalue?

Linear algebra is the cornerstone of many superior mathematical ideas and is extensively utilized in knowledge science, machine studying, laptop imaginative and prescient, and engineering. One of many elementary ideas of linear algebra is eigenvectors, usually mixed with eigenvalues. However what precisely is an eigenvector and why is it so essential?

This text breaks down the idea of eigenvectors in a easy and intuitive approach, making it simple for anybody to grasp.

What’s an eigenvector?

A sq. matrix is ​​related to a particular kind of vector known as an eigenvector. When the matrix acts on the eigenvector, it retains the path of the eigenvector unchanged and solely scales it by a scalar worth known as the eigenvalue.

In mathematical phrases, for a sq. matrix A, a nonzero vector v is an eigenvector if:

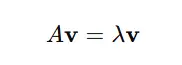
Right here:

• A is the matrix.
• v is the eigenvector.
• λ is the eigenvalue (a scalar).

Instinct behind eigenvectors

Think about you’ve gotten a matrix A that represents a linear transformation, similar to stretching, rotating, or scaling a 2D house. When this transformation is utilized to a vector v:

• Most vectors will change their path and magnitude.
• Nevertheless, some particular vectors will solely be scaled, however not rotated or inverted. These particular vectors are eigenvectors.

For instance:

• If λ>1, the eigenvector is stretched.
• If 0<λ<1, the eigenvector is compressed.
• If λ=−1, the eigenvector reverses its path however maintains the identical size.

Why are eigenvectors essential?

Eigenvectors play a vital function in varied mathematical and real-world functions:

1. Principal Part Evaluation (PCA): PCA is a extensively used method for dimensionality discount. Eigenvectors are used to find out the principal elements of the info, which seize the utmost variance and assist determine a very powerful options.
2. Google Web page Rank: The algorithm that classifies internet pages makes use of eigenvectors of a matrix that represents the hyperlinks between internet pages. The principal eigenvector helps decide the relative significance of every web page.
3. Quantum Mechanics: In physics, eigenvectors and eigenvalues ​​describe the states of a system and its measurable properties, similar to power ranges.
4. laptop imaginative and prescient: Eigenvectors are utilized in facial recognition programs, significantly in strategies similar to Eigenfaces, the place they assist characterize photographs as linear mixtures of significant options.
5. Vibrational Evaluation: In engineering, eigenvectors describe the modes of vibration in buildings similar to bridges and buildings.

Easy methods to calculate eigenvectors?

To search out eigenvectors, observe these steps:

• Arrange the eigenvalue equation: Begin with Av=λv and rewrite as (A−λI)v=0, the place I is the identification matrix. Remedy for the eigenvalues: Discover the eigenvectors:
• Remedy eigenvalues: Calculate det⁡(A−λI)=0 to search out the eigenvalues ​​λ.
• Discover eigenvectors: Substitute every eigenvalue λ into (A−λI)v=0 and clear up for v.

Instance: eigenvectors in motion

Contemplate an array:

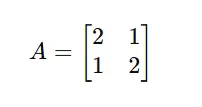
Step 1: discover eigenvalues ​​λ.

Remedy det⁡(A−λI)=0:

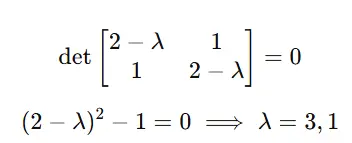
Step 2: Discover eigenvectors for every λ.

For λ=3:

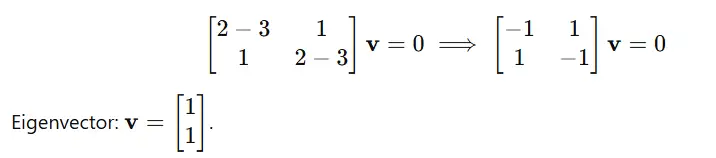
For λ=1:

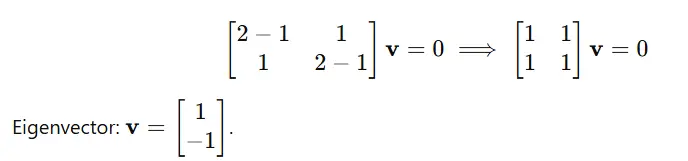
Python implementation

Let’s calculate the eigenvalues ​​and eigenvectors of a matrix utilizing Python.

Instance array

Contemplate the matrix:

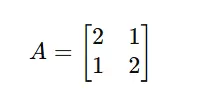
Code implementation

import numpy as np

# Outline the matrix
A = np.array(((2, 1), (1, 2)))

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)

# Show outcomes
print("Matrix A:")
print(A)

print("nEigenvalues:")
print(eigenvalues)

print("nEigenvectors:")
print(eigenvectors)

Manufacturing:

Matrix A:
((2 1)
 (1 2))

Eigenvalues:
(3. 1.)

Eigenvectors:
(( 0.70710678 -0.70710678)
 ( 0.70710678  0.70710678))

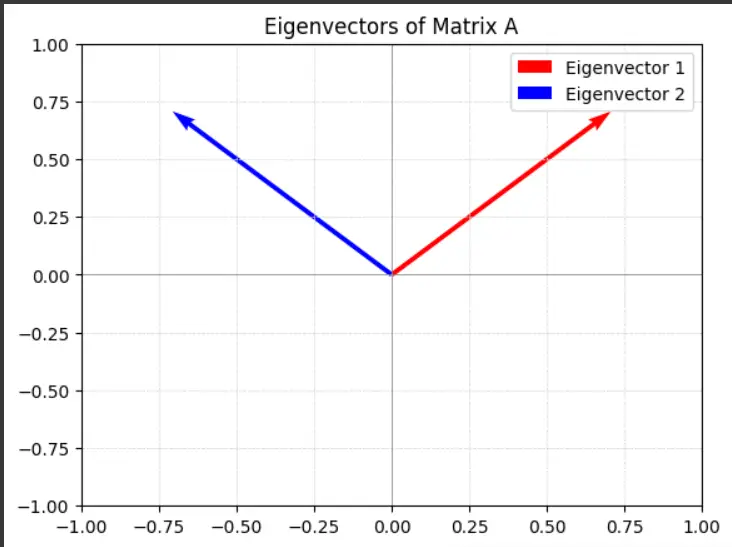
Visualizing eigenvectors

You’ll be able to visualize how the eigenvectors behave underneath the transformation outlined by matrix A.

Show code

import matplotlib.pyplot as plt

# Outline eigenvectors
eig_vec1 = eigenvectors(:, 0)
eig_vec2 = eigenvectors(:, 1)

# Plot authentic eigenvectors
plt.quiver(0, 0, eig_vec1(0), eig_vec1(1), angles="xy", scale_units="xy", scale=1, shade="r", label="Eigenvector 1")
plt.quiver(0, 0, eig_vec2(0), eig_vec2(1), angles="xy", scale_units="xy", scale=1, shade="b", label="Eigenvector 2")

# Modify plot settings
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.axhline(0, shade="grey", linewidth=0.5)
plt.axvline(0, shade="grey", linewidth=0.5)
plt.grid(shade="lightgray", linestyle="--", linewidth=0.5)
plt.legend()
plt.title("Eigenvectors of Matrix A")
plt.present()

This code will produce a graph exhibiting the eigenvectors of AAA, illustrating their instructions and the way they continue to be unchanged underneath the transformation.

Key takeaways

• Eigenvectors are particular vectors that stay in the identical path when remodeled by a matrix.
• They’re paired with eigenvalues, which decide how a lot the eigenvectors scale.
• Eigenvectors have essential functions in knowledge science, machine studying, engineering, and physics.
• Python offers instruments like NumPy to calculate eigenvalues ​​and eigenvectors simply.

Conclusion

Eigenvectors are a elementary idea in linear algebrawith highly effective functions in knowledge science, engineering, physics and extra. They characterize the essence of how a matrix transformation impacts sure particular instructions, making them indispensable in areas similar to dimensionality discount, picture processing, and vibrational evaluation.

By understanding and calculating eigenvectors, you unlock a strong mathematical software that permits you to clear up advanced issues with readability and precision. With strong Python libraries like NumPyExploring eigenvectors turns into simple, permitting you to visualise and apply these ideas in real-world situations.

Whether or not you’re constructing machine studying fashionsanalyzing structural dynamics or diving into quantum mechanics, a stable understanding of eigenvectors is a ability that may serve you properly in your journey.

Ceaselessly requested questions

Hello, I am Janvi, a knowledge science fanatic presently working at Analytics Vidhya. My journey into the world of information started with a deep curiosity about how we are able to extract significant insights from advanced knowledge units.